钢轨波磨是钢轨在投入使用后,随着运营时间的增加,在钢轨表面出现的周期性波浪状磨损现象[1].波磨会大大增强轮轨相互作用力,加速车辆和轨道各组成部件的损坏,增加养护维修费用.钢轨波磨是一个世界性的难题,这一现象得到国内外学者的广泛关注,在试验和理论方面均进行了大量的研究工作.王平等[2]建立了钢轨垂向/横向轮对轴扭转耦合模型,研究了轮对扭转振动对波磨的影响.刘涌涛等[3]基于长期跟踪测试结果及动力学分析理论对磨耗成因及发展趋势进行了研究.戴春阳等[4]基于有限元软件研究了钢轨磨耗的影响因素.张继业等[5]研究了轮对相互作用对波磨的影响,建立了波磨产生和发展的预测模型.刘学毅等[6]以磨耗功为参量对重载线路钢轨波磨进行了系统的研究.JIN等[7]通过足尺试验台再现了钢轨短波波磨,研究发现再现的钢轨波磨通过频率与模拟轨道的试验台的共振频率相近,表明波磨形成与轨道结构特性相关.Grassie等[8-9]综合了过往的波磨研究和工程实践,总结并完善了波磨的分类方法、特征、产生原因以及相应的治理措施.
随着城市轨道交通的迅速发展,钢轨波磨也越来越多地被发现,在直线段和曲线段上都有发生[10].现场调查发现,对于我国地铁大部分线路轨道采用的普通扣件轨道形式而言,钢轨波磨大部分出现在半径小于800 m的曲线段,波长大约为100~250 mm,波磨通过频率为50~140 Hz;大半径曲线段和直线段部分区域也出现了30~40 mm的短波长波磨,对应的通过频率为400~800 Hz[11].出现在直线轨道或大半径曲线轨道上的波磨,通常被称作响轨波磨或Pinned-Pinned共振波磨,这类波磨的不平整度虽然较小,但波长较短,车轮前进过程中沿轨道锤击,且只与波磨峰接触,其影响的大小可以是静态车轮负荷的几倍,因此这种波磨与轨道结构尤其是轨枕和紧固部件的快速损坏密切相关.
本文首先对上海某地铁线路上普通扣件轨道区段实测波磨进行特征分析,然后建立有限元模型进行模态分析,研究轨道固有频率特性与实测波磨的相关性.最后基于摩擦功的材料摩擦磨损模型,运用UM多体动力学软件,建立波磨叠加计算模型,并使用该模型分析波磨的频率特征与发展特性.
1 实测波磨与轨道结构特性的相关性分析 1.1 实测波磨的特性分析图 1为上海某地铁隧道整体道床普通扣件(DTVI2)地段钢轨实测波磨曲线.该区段线路曲率半径为3 000 m,隧道穿越土层结构为淤泥质黏土,沉降量较大.运营车辆为地铁A型车.

|
图 1 普通扣件轨道区段实测波磨 Fig.1 Measured corrugation of common fastener track section |
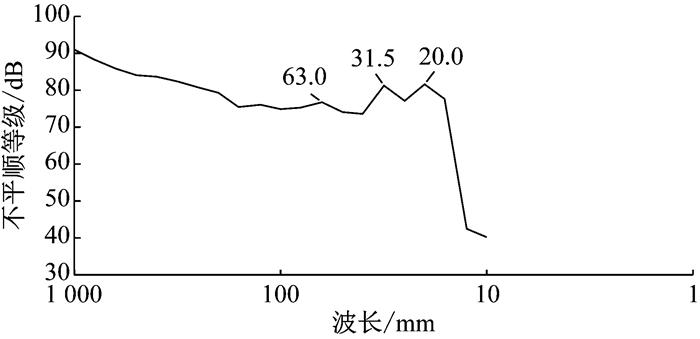
对实测波磨数据进行傅里叶变换,得到图 2所示波长不平顺等级的1/3倍频程图.波磨通常被认为是一种波长小于1 m的轨道不平顺[9],故此处1/3倍频程波长上限取为1 m.图中显示的短波波磨特征波长有20.0 mm、31.5 mm、63.0 mm.该区段车辆运行速度约为32 km·h-1,频率f=v/λ(其中v为车速,λ为波磨波长),则对应的通过频率分别为:444 Hz、282 Hz、141 Hz.
|
图 2 不平顺等级1/3倍频程 Fig.2 One-third octave of irregularity grade |
为了确定轨道的固有频率是否可能激发或强化上述实测数据中特征频率对应的波磨波长,通过建立有限元模型并结合模态分析,对轨道结构固有频率和钢轨波磨波长的关系进行研究.
1.2.1 有限元模型理论上,轨道上任一点受到的作用力的效果会传递到轨道系统的无穷远处.但在实际中,作用力的影响会随着距离的增加发生衰减,在超过某一范围后,该作用力的影响便可以忽略不计.对于移动荷载情形,较合适的轨道计算长度为100 m,当其大于100 m之后,计算结果几乎不受影响[12].
在保证工程精度和避免计算量过大的前提下,利用有限元软件ABAQUS建立了扣件间隔为0.625 m、轨道总长度为100 m的普通扣件(DTVI2)轨道结构的三维实体有限元模型,如图 3所示.其中钢轨为60 kg·m-1,轨道结构参数如表 1所示[13].钢轨和轨道板采用三维实体单元模拟,扣件系统、道床板与地基的连接均采用弹簧和阻尼单元模拟.由于轨道结构的对称性,选取轨道结构一半进行计算分析,即考虑一根钢轨和一半的道床板,并在道床板中心处设置对称约束,道床板断面尺寸为1 350 mm×300 mm.

|
图 3 普通扣件轨道有限元模型示意 Fig.3 The finite element model for common fastener track |
| 下载CSV 表 1 普通扣件轨道结构参数 Tab.1 Common fastener track structure parameters |
模态分析通常用于分析系统的固有频率属性.根据Grassie[9]的理论,波磨通常具有固定频率特征,因此在分析波磨时,轨道结构的振动特性通常被认为是引起特定频率波磨的主要原因.
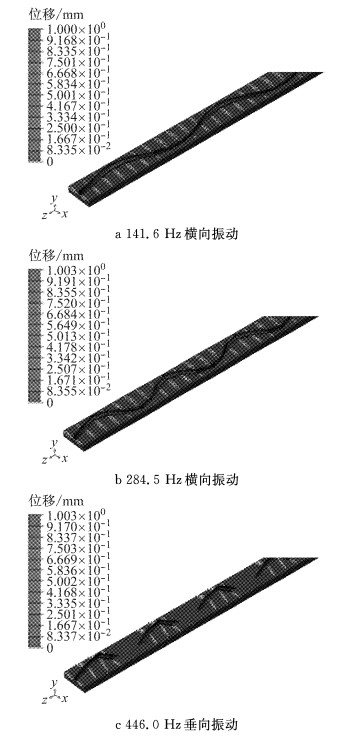
通过对上述模型进行模态分析,可以得到普通扣件轨道结构的固有频率及对应的各阶振型.结合实测部分得到的典型通过频率(141 Hz、282 Hz、444 Hz),与其接近的振型如图 4所示.
|
图 4 振型图 Fig.4 Mode diagram |
通过将计算得到的实测波磨典型特征频率与轨道结构的模态分析结果进行对比可知:141.6 Hz、284.5 Hz的固有频率对应轨道结构在横向的弯曲振动频率,该频率与现场波磨通过频率141 Hz、281 Hz相近;446.0 Hz的固有频率对应轨道结构在垂向的弯曲振动频率,该频率与现场波磨通过频率444 Hz相近.分析认为轨道结构可能在该特定频率处发生共振,从而导致对应波长钢轨波磨的产生.
2 基于摩擦功理论的磨耗计算模型 2.1 车辆模型由于研究对象为地铁线路上的波磨,故车辆模型采用地铁车辆的各项参数,参数取值如表 2所示,模型示意图如图 5所示.
| 下载CSV 表 2 车辆参数 Tab.2 Vehicle parameters |

|
图 5 车辆系统模型示意 Fig.5 Vehicle system model |
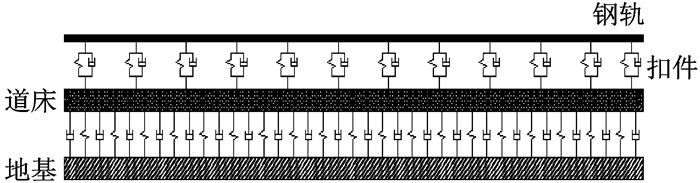
为更准确地描述轨道特性,采用柔性轨道模型.钢轨模型采用考虑剪切变形的Timoshenko梁,其能较好地体现高频振动的影响,适用于研究钢轨波磨问题.扣件部分采用Bushing力元进行模拟.道床板部分通过有限元软件建立三维实体单元模型并导入到UM前处理中,作为动力学模型的一个子系统,道床板断面尺寸2 700 mm×300 mm,长度60 m.道床板与地基的连接以及道床板与钢轨的连接都是通过定义力元进行模拟,可以考虑3个方向上的刚度和阻尼,连接部分各参数取值同表 1.轨道模型示意图如图 6所示.
|
图 6 普通扣件轨道模型示意 Fig.6 Common fastener track model |
在UM软件中,当轨道模型为柔性轨道时,采用Kik-Piotrowski接触模型进行仿真计算,该模型具有计算速度快、可靠性高的特点[14].对于法向接触有如下公式:
| $ \left. \begin{array}{l}{ N = \frac { \pi E \delta } { 2 ( 1 - \mu ^ { 2 } ) } ( \int _ { y _ { \rm r } } ^ { y _ {\rm l } } \int _ { - x _ { \rm l } } ^ { x _ { \rm l } } \frac { \sqrt { x _ { l } ^ { 2 } ( y ) - x ^ { 2 } } } { \sqrt { x ^ { 2 } + y ^ { 2 } } } {\rm d} x {\rm d} y ) ^ { - 1 } } \cdot \\{ \int _ { y _ { \rm r } } ^ { y _ { \rm l } } \int _ { - x _ { \rm l } } ^ { x _ {\rm l } } \sqrt { x _ { \rm l } ^ { 2 } ( y ) - x ^ { 2 } } {\rm d} x {\rm d} y }\end{array} \right. $ | (1) |
| $ p _ { 0 } = N \sqrt { 2 R \delta _ { 0 } } ( \int _ { y _ {\rm r } } ^ { y _ { \rm l } } \int _ { - x _ { \rm l } } ^ { x _ { \rm l } } \sqrt { x _ { \rm l } ^ { 2 } ( y ) - x ^ { 2 } } {\rm d} x { \rm d} y ) ^{-1} $ | (2) |
式中:N为法向力;E为杨氏模量;δ为轮轨之间的法向刚体穿透量;μ为材料的泊松比;xl(y)为接触面积互穿区域的前后边缘的坐标,xl(y)≈
对于切向接触,根据FASTSIM算法,从忽略接触区滑移的线性理论的主要假设出发,导出切向应力p(x, y)分布的形式如下:
| $ {{p}_{x}}\left( x, y \right)=\frac{1}{L}(x-{{x}_{\text{l}}})({{\nu }_{x}}-y\varphi ) $ | (3) |
| $ {{p}_{y}}\left( x, y \right)=\frac{1}{L}(\left[ x-{{x}_{\text{l}}}){{\nu }_{y}}+\frac{1}{2}({{x}^{2}}-{{x}^{2}_{\text{l}}})\varphi \right] $ | (4) |
式中:νx、νy、φ为纵向、横向和自旋蠕滑率;L为接触区域的弹性参数值;根据切向应力可以计算纵横向蠕滑力Fx、Fy.在接触区域对式(3)、(4)进行积分,可得蠕滑力公式如下:
| $ \left. \begin{array}{l}{ F _ { x } = \frac {\rm l } { L } \int _ { y _ {\rm r } } ^ { y _ {\rm l } } \int _ { - x _ {\rm l } } ^ { x _ {\rm l } } p _ { x } ( x , y ) {\rm d} x {\rm d} y = }\\ \qquad{ - \frac { 4 R } { L } \nu _ { x } \int _ { y _ {\rm r } } ^ { y _ {\rm l } } g ( y ) {\rm d} y + \frac { 4 R } { 3 L } \varphi \int _ { y _ {\rm r } } ^ { y _ {\rm l } } y g ( y ) {\rm d} y }\end{array} \right. $ | (5) |
| $ \left. \begin{array}{l}{ F _ { y } = \frac {\rm l } { L } \int _ { y _ {\rm r } } ^ { y _ {\rm l } } \int _ { - x _ {\rm l } } ^ { x _ {\rm l } } p _ { y } ( x , y ) {\rm d} x {\rm d} y = }\\ \qquad{ - \frac { 4 R } { L } \nu _ { y } \int _ { y _ {\rm r } } ^ { y _ {\rm l } } g ( y ) {\rm d} y - \frac { 4 \sqrt { 2 } } { 3 L _ { i } } \varphi \int _ { y _ {\rm r } } ^ { y _ {\rm l } } [ R g ( y ) ] ^ { 3 / 2 } {\rm d} y }\end{array} \right. $ | (6) |
除上述蠕滑力外,轮轨间也会产生一个绕z轴的力矩Mz,但是与由左右车轮的纵向蠕滑力的差所产生的旋转力矩相比非常小,故通常忽略不计.
2.4 基于摩擦功理论的磨耗计算模型采用基于摩擦功理论的摩擦磨损计算模型计算钢轨表面磨耗,该模型能够考虑自旋效应对磨耗的影响.假定在较短的时间步长Δt内,摩擦功率保持不变,则摩擦功W计算公式如下:
| $ W=P\Delta t $ | (7) |
式中:P为接触区域内的摩擦功率,为接触区域内各点上各个方向的蠕滑力与蠕滑率乘积的总和,如式(8)所示:
| $ P={{F}_{x}}{{\nu }_{x}}+{{F}_{y}}{{\nu }_{y}}+{{M}_{z}}\varphi $ | (8) |
在UM软件中,仿真计算可以输出任意时刻接触区域内的摩擦功率,能够计算出相应时间步长内的摩擦功,进而计算出该时刻的总磨耗质量.
材料磨损方面应用Archard的磨耗模型.在x位置处产生的磨耗总质量Δm可以表示为
| $ \Delta mx=KW\left( x \right) $ | (9) |
式中:K为磨耗比例系数,取1×10-9 kg·(N·m)-1.故可计算得到该时刻对应位置的钢轨表面的磨耗深度d(x).
| $ \text{d}\left( x \right)=\frac{\Delta m\left( x \right)}{A\rho } $ | (10) |
式中:A为接触区域面积;ρ为钢轨材料的密度,取7 800 kg·m-3.对于单节车厢,在轨道上某一特定位置xs处有
| $ D({{x}_{\text{s}}})=4\text{d}({{x}_{\text{s}}}) $ | (11) |
式中:D(xs)为单次运行得到的xs位置处的磨耗深度.将其作为不平顺加在钢轨表面上再次进行仿真计算,即可得到前次磨耗影响下的下一次的磨耗量,重复该过程,即可得到多次运行下钢轨表面的叠加磨耗.
3 波磨发展特性基于上述磨耗计算模型,使用UM软件进行波磨仿真计算,对波磨的频率特征和发展特性进行分析研究.
3.1 频率特征分析在进行波磨分析时,采用通过频率来表明波磨的频域特征.由于单次磨耗量比初始不平顺量级小得多,因此,为研究磨耗的特性,在初始条件下设定不平顺为零,即排除初始不平顺的影响.图 7为普通扣件轨道计算得到的磨耗量的频谱特征,其纵坐标转换为振级形式(均取左轨),分别是车速为80km·h-1、60 km·h-1、40 km·h-1的计算结果.

|
图 7 频谱特征 Fig.7 Spectrum characteristics |
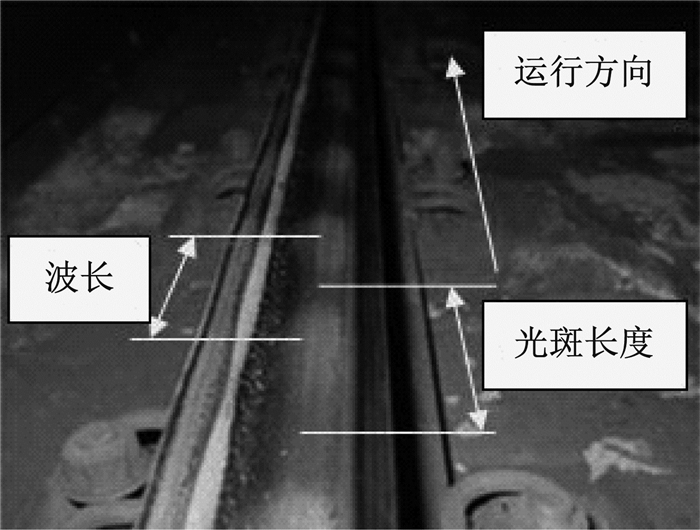
将图 7中标出的主要峰值频率汇总于表 3.对比分析可以得出,普通扣件轨道低频处峰值较大,而不同车速下峰值频率基本吻合,说明速度改变并未引起轨道特征频率发生改变,体现了波磨的固定频率特性.因此,在车速确定的情况下,可以得到波磨的显著波长范围.从现场照片(图 8)可见,波磨的光斑具有一定长度,因此在实际测量波长时,通常取值为两相邻光斑中心间距离,其值近似是一个平均波长的概念.
| 下载CSV 表 3 普通扣件轨道特征频率 Tab.3 Characteristic frequency of common fastener track |
|
图 8 轨道表面波浪形磨耗 Fig.8 Corrugation on track surface |
前文实测数据中计算得到的波磨典型通过频率141 Hz、282 Hz和444 Hz,与计算结果中的146 Hz、282 Hz和441 Hz(车速40 km·h-1)3个峰值频率相接近,说明在实测的轨道中,这些通过频率对应的波磨最终产生并得到发展.
3.2 发展特性分析由于单次计算的磨耗量极小,在普通扣件轨道上以100 000次为一个量级,按照8列编组每日运行260次计算,达到该程度的波磨约需要48 d.输出5个量级的叠加磨耗及其1/3倍频程曲线如图 9所示.其中图 9a、9b为车速80 km·h-1下的叠加过程,图 9c、9d为车速60 km·h-1下的叠加过程, 图 9e、9f为车速40 km·h-1下的叠加过程.曲线图对比可以得出,在相同速度下,随着叠加次数的增加,波磨波峰波谷会在轨道上固定位置叠加,同时波磨的主要通过频率会在40 Hz频带内产生,次要通过频率则产生在80 Hz频带内;在不同速度下,波磨的特征频率并未随速度的改变而发生改变.反映了波磨固定位置和固定频率的特性.由图 9b、9d和9f可见,在车速80km·h-1和60 km·h-1下, 40 Hz、80 Hz频带内波磨等级明显高于中高频对应的波磨等级,说明波磨在该频率处发生的可能性较大;而在车速40 km·h-1下,高频区域波磨等级相对较大,且变化平缓,说明在该车速下,轨道上主要表现为均匀磨耗.

|
图 9 波磨特征 Fig.9 Corrugation characteristic |
图 10为3种速度下主要频率40 Hz处的磨耗量等级发展趋势对比图.在80 km·h-1车速下,波磨等级从82.9 dB增加到99.4 dB,增量为16.5 dB;在60 km·h-1车速下,波磨等级从78.6 dB增加到95.1 dB,增量为16.5 dB;在40 km·h-1车速下,波磨等级从74.3 dB增加到83.1 dB,增量为8.8 dB.可以认为,车速对波磨的增长有一定影响,速度越大,总体磨耗量越大;但磨耗的发展速度不完全随车速增大而增大,在80 km·h-1和60 km·h-1条件下,波磨发展速度基本相同,40 km·h-1条件下则明显变小.

|
图 10 磨耗量等级对比 Fig.10 The wear volume level comparison |
(1) 对上海某地铁线路上特定区段的钢轨波磨实测数据进行了分析,得到了普通扣件轨道区段的典型通过频率有141 Hz、282 Hz、444 Hz.通过模态分析,发现实测波磨均存在与之频率相接近的轨道结构弯曲振型,列车运行可能激发了这些频率处的轨道结构共振,进而产生波磨.
(2) 基于磨耗计算模型进行仿真计算,研究了波磨的频率特征和发展特性.分析得到普通扣件轨道低频处峰值较大,而且不同车速下峰值频率基本吻合.通过对比磨耗叠加图及1/3倍频程等级图,可得相同速度下,随着叠加次数的增加,波磨波峰波谷叠加位置相同,特征频率相同;不同速度下,波磨的特征频率并未随速度的改变而发生改变;体现了波磨固定位置和固定频率的特性.同时在车速80km·h-1和60 km·h-1下,波磨在40 Hz、80 Hz频带内发生的可能性较大;而在车速40 km·h-1下,轨道上主要表现为均匀磨耗.
(3) 通过对比3种速度下主要频率40 Hz处的磨耗量等级发展趋势可知,车速对波磨的增长有一定影响,速度越大,总体磨耗量越大,但磨耗的发展速度不完全随车速增大而增大.
| [1] |
温泽峰.钢轨波浪形磨损研究[D].成都: 西南交通大学, 2006. WEN Zefeng. Study on rail corrugation[D]. Chengdu: Southwest Jiaotong University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10613-2006091833.htm |
| [2] |
王平, 刘学毅, 万复光. 轮轴扭转振动与曲线地段钢轨波形磨耗[J]. 西南交通大学学报, 1996, 31(1): 58 WANG Ping, LIU Xueyi, WAN Fuguang. Torsional vibration of wheelsets and curved rail corrugations[J]. Journal of Southwest Jiaotong University, 1996, 31(1): 58 |
| [3] |
刘涌涛, 刘文涛. 广州地铁道岔群磨耗的成因研究及治理措施[J]. 都市快轨交通, 2004, 17(4): 40 LIU Yongtao, LIU Wentao. The abrasion causes and treatments of the turnout group in Guangzhou metro[J]. Urban Rapid Rail Transit, 2004, 17(4): 40 DOI:10.3969/j.issn.1672-6073.2004.04.011 |
| [4] |
戴春阳, 胡华锋, 高亮, 等. 地铁运营条件与线路参数对曲线钢轨磨耗的影响[J]. 都市快轨交通, 2011, 24(5): 6 DAI Chunyang, HU Huafeng, GAO Liang, et al. Simulation study on metro operation and line parameters affecting rail wear on curves[J]. Urban Rapid Rail Transit, 2011, 24(5): 6 DOI:10.3969/j.issn.1672-6073.2011.05.003 |
| [5] |
张继业, 金学松, 张卫华. 基于高频轮轨作用的波浪型磨损研究[J]. 应用力学学报, 2004, 21(4): 6 ZHANG Jiye, JIN Xuesong, ZHANG Weihua. Rail corrugation at high frequency wheel-rail interaction[J]. Chinese Journal of Applied Mechanics, 2004, 21(4): 6 DOI:10.3969/j.issn.1000-4939.2004.04.002 |
| [6] |
刘学毅, 王平, 万复光. 重载线路钢轨波形磨耗成因研究[J]. 铁道学报, 2000, 22(1): 98 LIU Xueyi, WANG Ping, WAN Fuguang. Formation mechanism of rail corrugations in heavy-haul rail line[J]. Journal of the China Railway Society, 2000, 22(1): 98 DOI:10.3321/j.issn:1001-8360.2000.01.021 |
| [7] |
JIN X, WEN Z. Rail corrugation formation studied with a full-scale test facility and numerical analysis[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2007, 221(6): 675 DOI:10.1243/13506501JET269 |
| [8] |
GRASSIE S L, KALOUSEK J. Rail corrugation: Characteristics, causes and treatments[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1993, 207(1): 57 DOI:10.1243/PIME_PROC_1993_207_227_02 |
| [9] |
GRASSIE S L. Rail corrugation: Characteristics, causes, and treatments[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2009, 223(6): 581 DOI:10.1243/09544097JRRT264 |
| [10] |
金学松, 李霞, 李伟, 等. 铁路钢轨波浪形磨损研究进展[J]. 西南交通大学学报, 2016, 51(2): 264 JIN Xuesong, LI Xia, LI Wei, et al. Review of rail corrugation progress[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 264 DOI:10.3969/j.issn.0258-2724.2016.02.006 |
| [11] |
李伟.地铁钢轨波磨成因及其对车辆/轨道行为的影响[D].成都: 西南交通大学, 2015. LI Wei. Study on root cause of metro rail corrugation and its influence on behaviour of vehicle-track system[D]. Chengdu: Southwest Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10613-1017022324.htm |
| [12] |
翟婉明. 车辆轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2007 ZHAI Wanming. Vehicle-track coupled dynamics[M]. 4th ed. Beijing: Science Press, 2007 |
| [13] |
李霞.地铁钢轨波磨形成机理研究[D].成都: 西南交通大学, 2012. LI Xia. Study on the mechanism of rail corrugation on subway track[D]. Chengdu: Southwest Jiaotong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1014251545.htm |
| [14] |
PIOTROWSKI J, KIK W. A simplified model of wheel/rail contact mechanics for non-Hertzian problems and its application in rail vehicle dynamic simulations[J]. Vehicle System Dynamics, 2008, 46(1/2): 27 |
 2019, Vol. 47
2019, Vol. 47

