2. 上海海事大学 交通运输学院,上海 201306
2. College of Transport and Communications, Shanghai Maritime University, Shanghai 201306, China
固定交通检测器的数据采集缺失现象对交通数据分析和挖掘等均带来不利的影响,因此有必要进行缺失数据修复.常见的数据修复方法有历史均值法[1-3]、插值法[4-5]、主成分分析法[6-8]、时间序列法[9]及机器学习算法[10-11].历史均值法是最早发展起来的数据修复方法.陆化普等[1]提出了基于历史数据和当前数据加权平均的数据修复方法.姜桂艳等[2]利用相邻时段及路段数据对故障数据进行修复.孙玲等[3]基于缺失数据的时空相关性将相关数据加权重构作为缺失数据的修复值.插值法主要分为指数平滑法、样条插值法及回归方法.Smith等[4]基于相邻时段数据的指数平滑值进行故障数据修复.Boyles[5]比较了简单线性回归模型、多元线性回归模型、局部和全局回归模型、非正态贝叶斯线性回归模型等方法后指出, 虽然回归算法简单且容易构建,但是数据修复结果在不同交通状态下不可靠.Qu等[6-7]和Li等[8]提出了概率主成分分析法、贝叶斯主成分分析法及核概率主成分分析法,指出该类方法数据修复精度优于历史均值法及样条插值法.ARIMA(autoregressive integrated moving average model)是常用的时间序列数据修复方法.Ghosh等[9]比较了ARIMA与Holt-Winters指数平滑数据修复方法及随机游走算法,指出ARIMA是一种有效的数据修复方法.近几年,机器学习模型也逐渐应用于缺失数据修复.Tang等[10]提出基于模糊C均值与遗传算法相结合的数据修复方法.Zhang等[11]衡量同一时刻不同地点交通参数的相关性,并提出基于最小二乘支持向量回归的缺失数据修复方法.
对于上述数据修复模型,选择解释变量时的主要依据为交通流数据的时空相关性,所有检测器均采用固定的解释变量,但是不同检测器数据与同一相关序列的相关性存在较大差异,解释变量固定势必影响部分检测器缺失数据的修复精度,而且数据的连续缺失容易导致修复误差的逐步传递和累积.另外,一个有效的数据修复方法既要考虑交通流数据的周期变化特性,又要捕捉复杂交通环境引起的交通流数据的实时变化,这对目前的研究仍具有较大的挑战.为避免连续数据缺失造成的误差累积,基于数据的相关性及连续缺失情况为修复方法动态地选择解释变量,并综合考虑交通流数据的周期性变化趋势和实时变化特性,提出一种改进的数据修复方法.
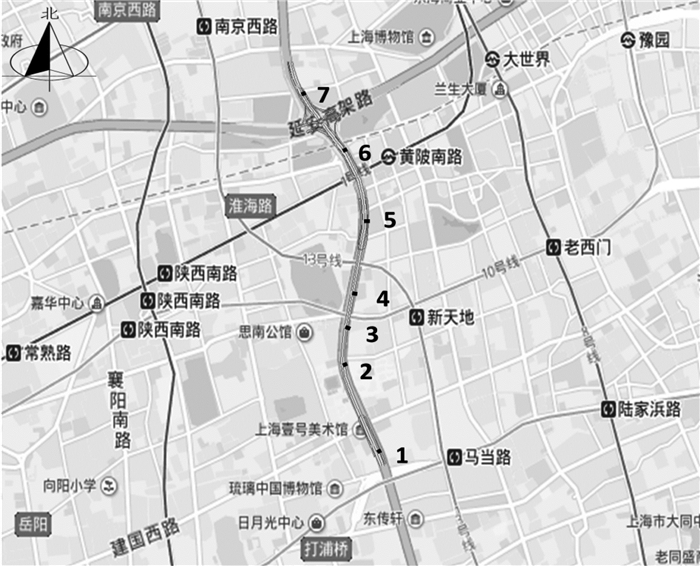
1 数据来源本研究选取的数据为2017年3月6日—31日上海市南北高架东侧徐家汇路至大沽路路段20个工作日内固定检测器采集的流量数据.该段快速路长度约为3 km,单向四车道,设计车速为80 km·h-1.主线共布设了7组完好的固定检测器,采集字段为检测器编号、采集时间、流量、平均速度、平均时间占有率等.其中,流量为5 min内经过检测器所处断面的车流量总数.为满足交通管理实时控制的需求,对修复时段t的缺失数据,仅采用历史时段(t-h)(h≥1)的数据进行修复.为方便说明,将分析范围内的检测器重新编号,从南向北方向行驶的车辆依次经过的检测器为1号至7号.检测器空间位置分布如图 1所示.
|
图 1 上海市南北高架检测器分布 Fig.1 Detectors on the north-south viaduct in Shanghai |
所提出的综合数据修复方法将检测器采集的流量数据分成两部分, 即周期性变化趋势与实时变化残差值.描述周期性特征的函数主要有三角级数法[12]、简单平均值法(SAM)[13]及双指数平滑法[14].选择简单且常用的简单平均值法进行周期性变化趋势描述,采用动态选择解释变量的支持向量回归(DV-SVR)算法进行实时变化残差值的预测.下文称所提出的综合数据修复方法为SAM-DV-SVR,计算式如下所示:
| $ Y(t) = D(t) + R(t) $ | (1) |
式中:Y(t)为t时段检测器采集的流量实际值;D(t)为流量数据的周期性部分;R(t)为残差值.
2.1 简单平均值法周期分析图 2为3号检测器2017年3月份一周工作日的流量数据分布.可以非常明显地看出, 流量数据呈现出以24 h为一个周期的反复特性.计算每个检测器3月份任意2个工作日的数据相关系数,并进一步得到相关系数均值,该均值可以反映检测器的日变化趋势的一致性.计算得出3号、4号、5号检测器的流量数据相关系数均值分别为0.978、0.927、0.944, 可以看出3号检测器流量数据的日变化趋势更为相似.假设连续采集N天的工作日数据,每天采集样本数为n, 每天采集的流量数据可记为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Y}}_1} = \left( {{Y_1}(1),{Y_1}(2),{Y_1}(3), \cdots ,{Y_1}(n)} \right)}\\ {\; \vdots }\\ {{\mathit{\boldsymbol{Y}}_N} = \left( {{Y_N}(1),{Y_N}(2),{Y_N}(3), \cdots ,{Y_N}(n)} \right)} \end{array}} \right. $ | (2) |

|
图 2 工作日流量的周期性分析 Fig.2 Periodic analysis of flow on weekdays |
简单平均值法计算式为
| $ D\left( t \right) = \frac{1}{N}\sum\limits_{r = 1}^N {{Y_r}\left( t \right)} $ | (3) |
本研究选取3月6日至3月22日的13个工作日的数据计算周期趋势,因此N=13, n=288.
2.2 动态选择解释变量的支持向量回归模型 2.2.1 备选相关序列构建每个检测器每天采集的流量数据可组成288维的向量,将缺失数据所在的向量称为目标向量S,而由相关数据组成的向量称为相关序列.根据以往研究结论[15],共选择了8个备选相关序列,如表 1所示.将目标向量S分别与相关序列S1至S8进行相关系数计算,可分别得到目标向量与各相关序列的相关系数,将相关系数的大小作为缺失数据修复模型解释变量的重要选择依据.相关系数计算式为
| $ {R_a} = \frac{{\sum\limits_{j = 1}^n {\left( {S\left( j \right) - \bar S} \right)\left( {{S_a}(j) - \overline {{S_a}} } \right)} }}{{\sqrt {\sum\limits_{j = 1}^n {{{\left( {S\left( j \right) - \bar S} \right)}^2}} \sum\limits_{j = 1}^n {{{\left( {{S_a}(j) - \overline {{S_a}} } \right)}^2}} } }} $ | (4) |
| 下载CSV 表 1 相关序列描述 Tab.1 Description for correlation sequences |
式中:Ra为目标向量S与相关序列Sa的相关系数;a=1, 2, …, 8;S(j)为目标向量S的第j个采样数据,Sa(j)为相关序列Sa的第j个采样数据; S与
为充分考虑流量数据的时空相关性,解释变量的选择至少包括一个时间相关序列向量及一个空间相关序列向量.解释变量动态选择的依据一是目标向量与相关序列向量相关系数的大小,二是连续缺失数据的数量.首先,构建相关序列S1至S8,若数据存在连续缺失现象,如检测器(t-1)时段及t时段数据均缺失,则由(t-2)时段数据作为相关序列S1,记为S1, 2,(t-3)时段数据作为相关序列S2,记为S2, 3,依次类推; 然后, 计算相关系数R1至R8,根据相关系数大小选择解释变量来进行缺失数据修复.解释变量选择流程如图 3所示.图 3中,m为解释变量的数量.

|
图 3 解释变量选择流程 Fig.3 Flow chart of explanatory variable selection |
设训练样本集M={(yi, Va, i, Vb, i, Vc, i, Vd, i), i=1, …, l}, 其中Va, i、Vb, i、Vc, i、Vd, i为动态选取的输入变量,yi为相应的输出值,本研究中yi为目标检测器的缺失数据,l为训练样本个数.支持向量回归模型的基本思想是寻找一个从输入空间到输出空间的非线性映射函数φ(x),通过该函数将训练样本集映射到高维特征空间P,因此可在空间P中对原始问题进行线性回归[16].映射关系如下所示:
| $ f\left( x \right) = \left( {\mathit{\boldsymbol{w}} \cdot \mathit{\boldsymbol{\varphi }}\left( x \right)} \right) + b,\;\;\;\;\mathit{\boldsymbol{w}} \in P $ | (5) |
式中:w为权重值;(·)为内积运算;b为偏置项.w和b通过最小化下列函数进行估计:
| $ R\left( \mathit{\boldsymbol{w}} \right) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + C\sum\limits_{i = 1}^l {{H_\varepsilon }\left( {Y\left( t \right),\hat Y\left( t \right)} \right)} $ | (6) |
式中:Y(t)为真实值;Ŷ(t)为输出值; ε为不敏感代价函数定义的误差; Hε(Y(t), Ŷ(t))为ε不敏感损失函数; C为惩罚系数.Hε(Y(t), Ŷ(t))的定义如下所示:
| $ \begin{array}{l} {H_\varepsilon }\left( {Y\left( t \right),\hat Y\left( t \right)} \right) = \\ \left\{ {\begin{array}{*{20}{l}} {\left| {Y\left( t \right) - \hat Y\left( t \right)} \right| - \varepsilon ,\;\;\;\;\left| {Y\left( t \right) - \hat Y\left( t \right)} \right| > \varepsilon }\\ {0,\;\;\;\;\;\;其他} \end{array}} \right. \end{array} $ | (7) |
式(7)表明, 若SVR输出值Ŷ(t)与真实值Y(t)差的绝对值小于设定的ε时,损失函数值忽略不计;否则, 损失函数值大小为|Y(t)-Ŷ(t)|超出ε的部分.引入核函数,将式(6)与(7)转换为求解下式:
| $ \begin{array}{l} \min \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}} + C\sum\limits_{i = 1}^l {{\xi _i}} + C\sum\limits_{i = 1}^l {\xi _i^*} \\ {\rm{s}}.\;{\rm{t}}.\;\;\;{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right) + b - Y\left( t \right) \le \varepsilon + {\xi _i}\\ \;\;\;\;\;\;\;Y\left( t \right) - {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right) - b \le \varepsilon + \xi _i^*\\ \;\;\;\;\;\;\;{\xi _i},\xi _i^* \ge 0,\;\;\;\;i = 1, \cdots ,l \end{array} $ | (8) |
式中:ξi、ξi*为松弛变量.引入拉格朗日乘子对最优化问题进行求解,可得到权值计算式, 如下所示:
| $ \mathit{\boldsymbol{w}} = \sum\limits_{i = 1}^n {\left( {{\alpha _i} - \alpha _i^ * } \right)\mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right)} $ | (9) |
式中:αi、αi*为拉格朗日乘子,即最小化R(w)的解.αi、αi*必须满足
| $ \sum\limits_{i = 1}^l {{\alpha _i}} = \sum\limits_{i = 1}^l {\alpha _i^*} ,\;\;\;\;0 \le {\alpha _i},\alpha _i^* \le C,i = 1,2, \cdots ,l $ | (10) |
通过式(5)和式(9),可以将f(x)表示为
| $ \begin{array}{*{20}{c}} {f(x) = \sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)K\left( {{x_i},x} \right) + b} }\\ {K\left( {{x_i},x} \right) = \mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right) \cdot \mathit{\boldsymbol{\varphi }}(x)} \end{array} $ | (11) |
式中:K(xi, x)为核函数.核函数不同,模型决策函数的最终形式也不相同.SVR模型支持常见的线性、多项式、径向基(RBF)、Sigmoid等4种核函数,本研究选取最常用的RBF核函数.
在ε-SVR的构建时,常数C作为惩罚系数控制损失的大小,模型求解中C可作为调节参数,影响训练模型的分类性能.此外,RBF核函数中参数g的数值也会明显影响模型的预测性能.在参数设置过程中,采用网格分析法及交叉验证法对支持向量回归中的常数C及RBF核函数参数g进行参数寻优.交叉验证法为:将原始数据均分成3组,对每组子集数据做1次验证集,其中2组子集数据作为训练集,最后得到3个模型,用这3个模型最终验证集的分类准确率平均值作为性能评价指标.网格分析法是通过编程枚举的方式对不同参数下的模型预测效果进行对比.此处以数据缺失一个的情况为例介绍惩罚系数C及核函数参数g的选择对SVR模型的影响.该实验采用均方误差(αMSE)作为评价指标,计算公式为
| $ {\alpha _{{\rm{MSE}}}} = \frac{1}{{{n_1}}}\sum\limits_{t = 1}^{{n_1}} {{{\left( {Y\left( t \right) - \hat Y\left( t \right)} \right)}^2}} $ | (12) |
式中:n1为修复数据个数.
图 4为惩罚系数C及核函数参数g对SVR模型预测结果的影响.从图 4可以看出,惩罚系数C较小时,SVR处于“欠学习”状态,预测误差并不是最小,随着C的增大,误差减小随后又逐渐增大,说明当C大于某一值后,SVR模型处于“过学习”状态.C在一定的区间内时,不同的取值得到的误差相差不大,说明对于固定的g, 存在多个C可以使得SVR模型取得较好的预测能力.同样,随着g的增大,预测均方误差呈现先减小后增大的两边大中间小的趋势,说明当g增大到一定程度之后,SVR模型呈现“过学习”现象.可见,g的变化对模型的预测能力也有非常大的影响.通过网格学习方法,遍历log2 C及log2 g 2个参数在-5到5之间的所有组合,选择最优的参数建立数据修复精度最高的回归模型.另外,针对不同的检测器选择及不同的解释变量输入,SVR模型依据网格分析法及交叉验证法对2个参数进行重新选择.

|
图 4 C与g对SVR模型的影响 Fig.4 Influence of C and g on SVR model |
选择编号为3号、4号、5号的检测器作为模型测试对象.将3月6日—10日(周一至周五)数据作为相关序列构建的基础数据,如3月13日缺失数据修复时的相关序列S4的构建需要使用3月6日的历史数据.3月13日—22日的8个工作日数据作为模型训练数据,用来进行模型参数的标定.3月23日—31日的7个工作日数据作为模型预测结果的测试数据,用来评价模型的泛化能力.如前所述,数据采集时不仅存在单个数据缺失现象,还存在连续数据缺失现象.选取的3月6日—31日3个检测器数据均为100%检测无缺失数据,将3月23日—31日的7天数据随机剔除10%的数据,分别构建连续缺失1~10个数据的场景进行数据修复,进而与采集的真实数据进行比较,从而验证模型的修复精度.数据修复精度评价指标包括平均绝对误差(βMAE)、平均绝对百分比误差(γMAPE)、均方根误差(δRMSE).3个指标的表达式如下所示:
| $ {\beta _{{\rm{MAE}}}} = \frac{1}{{{n_1}}}\sum\limits_{t = 1}^{{n_1}} {\left| {\hat Y\left( t \right) - Y\left( t \right)} \right|} $ | (13) |
| $ {\gamma _{{\rm{MAPE}}}} = \frac{1}{{{n_1}}}\sum\limits_{t = 1}^{{n_1}} {\left| {\frac{{\hat Y\left( t \right) - Y\left( t \right)}}{{Y\left( t \right)}}} \right|} $ |
| $ {\delta _{{\rm{RMSE}}}} = \sqrt {\frac{{\sum\limits_{t = 1}^{{n_1}} {{{\left( {Y\left( t \right) - \hat Y\left( t \right)} \right)}^2}} }}{{{n_1}}}} $ |
首先,基于第2.1节所述简单平均值法计算3个检测器的周期;其次,根据第2.2节所述方法构建8个相关序列来计算相关系数,并根据数据缺失情况及相关系数的大小动态选择解释变量;然后,基于支持向量回归模型预测缺失数据的残差值;最后,将预测的残差值与周期值相加组成缺失数据修复值.
(1) 解释变量动态选择
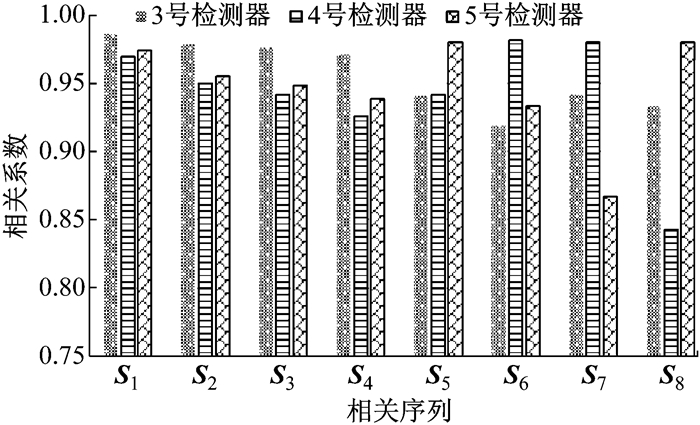
图 5为3个目标检测器仅缺失一个数据且相邻检测器的相关数据完整时构建的8个相关序列.可以看出,不同的检测器与同一个相关序列的相关系数差异较大.3号检测器与时间相关序列S1至S4的相关性明显高于空间相关序列S5至S8.与4号和5号检测器相关性最强的序列均为空间相关序列,4号检测器与S6、S7相关序列的相关性最大, 5号检测器与S5、S8相关序列的相关性最大.可以看出,为所有的检测器动态选择不同的解释变量是非常有必要的.
|
图 5 相关序列的相关系数 Fig.5 Correlation coefficients of correlation sequences |
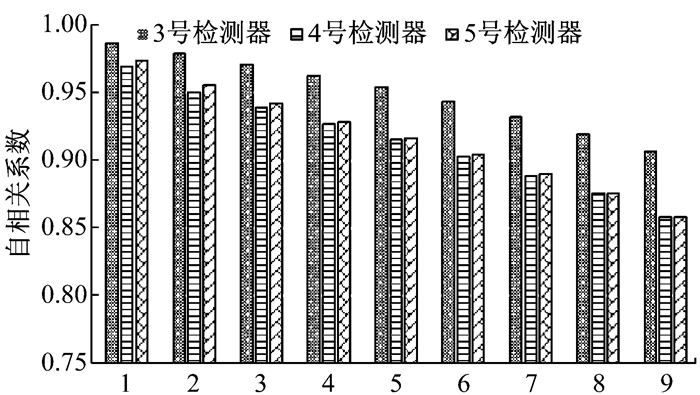
图 6为3个检测器的自相关系数.横坐标1至9代表的是(t-1)至(t-9)时段,纵坐标为t时段分别与(t-1)至(t-9)时段数据的相关系数.可以看出,随着时间距离的增加自相关系数逐渐减小.3号检测器数据的自相关系数明显大于4号与5号检测器的自相关系数.
|
图 6 检测器数据的自相关系数 Fig.6 Autocorrelation coefficients of detector data |
表 2为目标检测器连续缺失1~10个数据且相邻检测器数据完整、历史日期数据完整时解释变量的选择方案.因相邻检测器数据缺失或者历史日期数据缺失时解释变量的选择方案较多,故此处不予列出.可以看出,对于不同的检测器, 解释变量的选择存在较大差异.其中,Si, k表示选取的(t-k)时段数据作为相关序列Si,S1S2S3S7表示选择4个相关序列作为解释变量,分别为相关序列S1、S2、S3、S7.
| 下载CSV 表 2 解释变量选择结果 Tab.2 Selection results of explanatory variable |
(2) 支持向量回归模型
根据表 2中连续缺失1~10个数据的条件下解释变量的选择方案来动态选择模型的输入数据,如3号检测器某个需要修复的数据连续缺失数为1时,则选择S1、S2、S3、S74个相关序列的数据作为模型的输入数据,输出数据为缺失数据的残差值,再加上该时段对应的周期值得到缺失数据的修复值.表 3为3号检测器根据表 2选择不同解释变量时模型的惩罚系数C及核函数参数g的选择方案以及残差预测结果的平均绝对误差.可以看出,解释变量的动态选择,避免了预测误差随着连续缺失个数的增多而导致的误差累积现象.
| 下载CSV 表 3 SVR模型参数选择结果及数据修复平均绝对误差 Tab.3 Selection results of parameters and βMAE of SVR Model |
(3) 数据修复结果
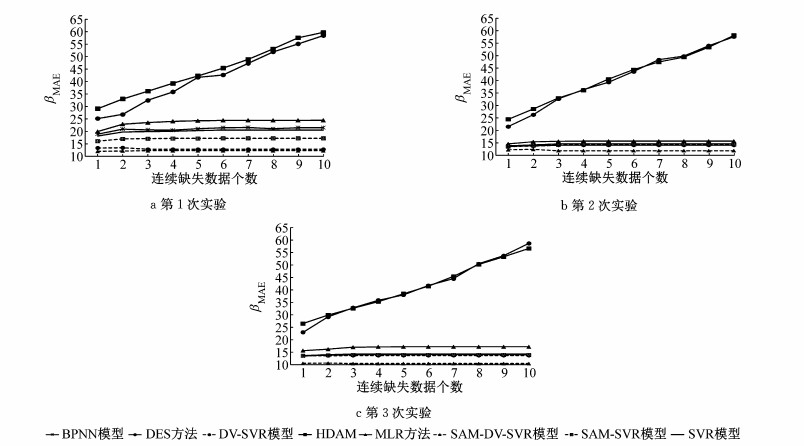
将以往研究中提出的数据修复方法与本研究提出的综合修复方法SAM-DV-SVR进行修复精度对比.参与对比的修复方法包括双指数平滑(DES)方法、常规SVR模型、历史数据平均方法(HDAM)、多元线性回归(MLR)方法、反向传播神经网络(BPNN)模型、仅考虑周期趋势的SVR(SAM-SVR)模型、仅考虑解释变量动态选择的SVR(DV-SVR)模型及本研究提出的综合数据修复模型SAM-DV-SVR.其中,历史数据平均法为同一检测器前4个时段值均值.常规SVR模型及MLR方法选取常用的4个解释变量作为预测模型输入,分别为目标检测器前2个时段数据(S1, S2)及前后断面同时刻数据(S5, S6).为保证模型的可对比性,本研究提出的综合模型同样选择4个解释变量.为排除模型预测结果的偶然性,随机剔除10%的数据并对结果验证过程进行了3次重复实验.图 7为5号检测器3次重复实验的平均绝对误差.可以看出,3次数据修复平均绝对误差虽然数值大小有所差异,但各模型数据修复精度的排名基本保持一致.从图 7还可以看出,HADM及DES方法因仅考虑了交通流数据的时间相关性,只采用本身检测器的历史数据作为解释变量,数据修复精度明显低于其他几种模型,并且随着数据缺失个数的增加,修复误差均明显增加.因此, 在下面的讨论中,仅对其他6种模型的数据修复结果取平均值进行深入分析.
|
图 7 5号检测器3次重复实验平均绝对误差 Fig.7 βMAE of 3 repeated experiments on No.5 detector |
图 8~10分别为6种模型的数据修复平均绝对误差、平均绝对百分比误差及均方根误差.分析3个检测器的数据修复结果, 可以看出:

|
图 8 不同连续缺失数据个数下6种模型修复平均绝对误差 Fig.8 βMAE of 6 models for different numbers of continuous missing data |
|
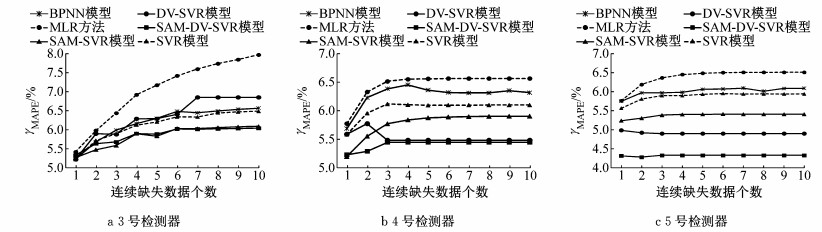
图 9 不同连续缺失数据个数下6种模型修复平均绝对百分比误差 Fig.9 γMAPE of 6 models for different numbers of continuous missing data |

|
图 10 不同连续缺失数据个数下6种模型修复均方根误差 Fig.10 δRMSE of 6 models for different numbers of continuous missing data |
(1) 相较于传统的SVR模型,SAM-DV-SVR模型对缺失数据修复的精度显著提升.
(2) 3号检测器中SAM-SVR模型预测精度明显优于DV-SVR模型,而4号及5号检测器则呈现相反的结论.原因为3号检测器工作日每天流量的周期性变化趋势更为一致,考虑周期性的SAM-SVR模型可充分利用流量数据的周期性更好地进行缺失数据的修复.同时, 3号检测器的时间相关序列的相关系数明显大于空间相关序列的相关系数,采用DV-SVR模型在数据连续缺失达到7个时会选择空间相关序列进行数据修复,数据修复精度明显较低.4号和5号检测器空间相关序列的相关性大于时间相关序列的相关性,采用动态变量的DV-SVR模型可选择相关性强的空间相关序列作为输入变量以提升缺失数据修复精度.
(3) SAM-DV-SVR模型对5号检测器的数据修复精度提升最为明显,相较于传统的SVR模型,在数据连续缺失1~10个的情况下,平均绝对误差平均减小了25.23%,而且平均绝对百分比误差均低于5%.原因为5号检测器的流量数据既具有较为一致的日变化趋势,又与相邻检测器的空间相关序列具有较强的相关性.因此, 相较于传统的SVR模型,考虑周期性的SAM-SVR模型可提升数据修复精度,动态选择解释变量的DV-SVR模型在数据连续缺失时也可利用相关性强的空间相关序列进行数据修复以保证缺失数据的修复精度.SAM-DV-SVR模型将上述2种因素进行综合考虑,因此可较大幅度地提升5号检测器的数据修复精度.
4 结语SAM-DV-SVR模型不仅为数据修复模型选择了最佳的解释变量,还综合考虑了交通流数据的周期性变化趋势和实时变化特征.与常用的几种数据修复模型在数据连续缺失1至10个的条件下数据修复精度的对比结果可以看出,SAM-DV-SVR模型体现了更高的数据修复精度.
目前仅验证了快速路交通流数据中的流量数据修复,未对普通道路的间断交通流数据进行模型应用验证,在后期研究中予以考虑.另外,本研究采集的数据为断面交通流数据,因此在空间相关序列选择时未考虑同一断面相邻车道情况,后续研究可补充该数据以进行模型的验证.
| [1] |
陆化普, 屈闻聪, 孙智源. 基于S-G滤波的交通流故障数据识别与修复算法[J]. 土木工程学报, 2015(5): 123 LU Huapu, QU Wencong, SUN Zhiyuan. Detection and repair algorithm of traffic erroneous data based on S-G filtering[J]. China Civil Engineering Journal, 2015(5): 123 |
| [2] |
姜桂艳, 江龙晖, 张晓东, 等. 动态交通数据故障识别与修复方法[J]. 交通运输工程学报, 2004(1): 121 JIANG Guiyan, JIANG Longhui, ZHANG Xiaodong, et al. Malfunction identifying and modifying of dynamic traffic data[J]. Journal of Traffic and Transportation Engineering, 2004(1): 121 DOI:10.3321/j.issn:1671-1637.2004.01.030 |
| [3] |
孙玲, 刘浩, 牛树云. 考虑时空相关性的固定检测缺失数据重构算法[J]. 交通运输工程学报, 2010(5): 121 SUN Ling, LIU Hao, NIU Shuyun. Reconstructive method of missing data for location-specific detector considering spatio-temporal relationship[J]. Journal of Traffic and Transportation Engineering, 2010(5): 121 DOI:10.3969/j.issn.1671-1637.2010.05.021 |
| [4] |
SMITH B L, SCHERER W T, CONKLIN J H. Exploring imputation techniques for missing data in transportation management system[J]. Transportation Research Record: Journal of the Transportation Research Board, 2003, 1836(1): 132 DOI:10.3141/1836-17 |
| [5] |
BOYLES S.A comparison of interpolation methods for missing traffic volume data[C]//Proceedings of the 90th Annual Meeting of the Transportation Research Board. Washington DC: Transportation Research Board, 2011: 23-27.
|
| [6] |
QU L, LI L, ZHANG Y, et al. PPCA-based missing data imputation for traffic flow volume: a systematical approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(3): 512 DOI:10.1109/TITS.2009.2026312 |
| [7] |
QU L, LI L, ZHANG Y, et al. A BPCA based missing value imputing method for traffic flow volume data[C]//Intelligent Vehicles Symposium. Eindhoven: IEEE, 2008: 985-990.
|
| [8] |
LI L, LI Y, LI Z. Efficient missing data imputing for traffic flow by considering temporal and spatial dependence[J]. Transportation Research, Part C: Emerging Technologies, 2013, 34: 108 DOI:10.1016/j.trc.2013.05.008 |
| [9] |
GHOSH B, BASU B, O'MAHONY M. Time-series modeling for forecasting vehicular traffic flow in Dublin[C]//Proceedings of the 84th Annual Meeting of Transportation Research Board. Washington DC: Transportation Research Board, 2005: 1-22.
|
| [10] |
TANG J, ZHANG G, WANG Y H, et al. A hybrid approach to integrate fuzzy C-means based imputation method with genetic algorithm for missing traffic volume data estimation[J]. Transportation Research, Part C: Emerging Technologies, 2015, 51: 29 DOI:10.1016/j.trc.2014.11.003 |
| [11] |
ZHANG Y, LIU Y. Missing traffic flow data prediction using least squares support vector machines in urban arterial streets[C]//Proceedings of the IEEE Symposium on Computational Intelligence and Data Mining. Nashville: IEEE, 2009: 76-83.
|
| [12] |
ZOU Y, HUA X, ZHANG Y, et al. Hybrid short-term freeway speed prediction methods based on periodic analysis[J]. Canadian Journal of Civil Engineering, 2015, 42(8): 570 DOI:10.1139/cjce-2014-0447 |
| [13] |
CHEN C, WANG Y, LI L, et al. The retrieval of intra-day trend and its influence on traffic prediction[J]. Transportation Research, Part C: Emerging Technologies, 2012, 22: 103 DOI:10.1016/j.trc.2011.12.006 |
| [14] |
TANG J, WANG H, WANG Y, et al. Hybrid prediction approach based on weekly similarities of traffic flow for different temporal scales[J]. Transportation Research Record:Journal of the Transportation Research Board, 2014, 2443(1): 21 DOI:10.3141/2443-03 |
| [15] |
陆百川, 郭桂林, 肖汶谦, 等. 基于多尺度主元分析法的动态交通数据故障诊断与修复[J]. 重庆交通大学学报:自然科学版, 2016(1): 134 LU Baichuan, GUO Guilin, XIAO Wenqian, et al. Fault diagnosing and modifying of dynamic traffic data based on MSPCA[J]. Journal of Chongqing Jiaotong University: Natural Science, 2016(1): 134 |
| [16] |
向昌盛.基于支持向量机的时间序列组合预测模型[D].长沙: 湖南农业大学, 2011. XIANG Changsheng. Time series combination prediction model based on support vector machine[D].Changsha: Hunan Agricultural University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10537-1012298480.htm |
 2019, Vol. 47
2019, Vol. 47

